Balancing the rapid convergence of NAG with the stability of SGD to engineer a dynamic, hybrid optimization algorithm.

The success of modern machine learning models relies heavily on how efficiently we can optimize complex, multi-parameter loss functions. While Deep Learning is the leading architecture today, the true engineering challenge lies in the optimization algorithms used to train them.

In my TÜBİTAK-2209A research project, I focused on two fundamental optimization methods: Stochastic Gradient Descent (SGD) and Nesterov Accelerated Gradient (NAG).

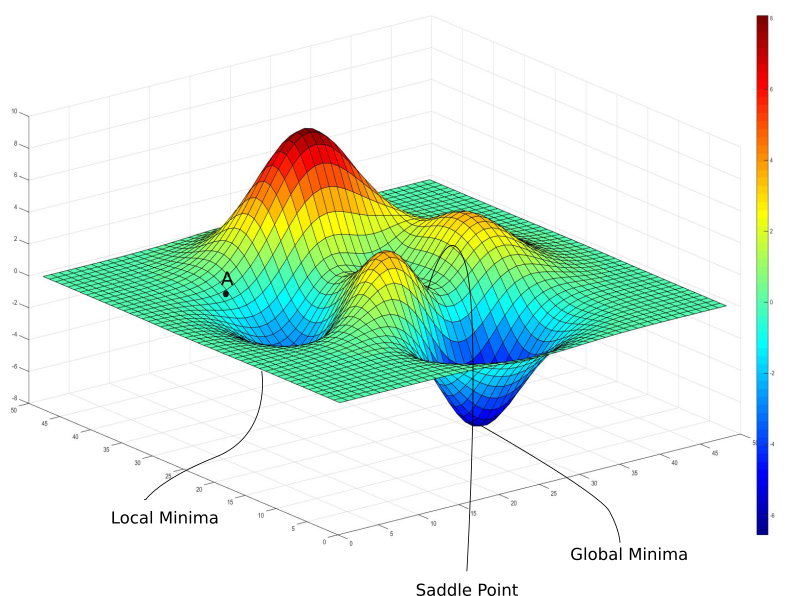Optimization Landscape (Note: Visualizing the complex topology of a loss function where algorithms must navigate to find the global minimum.)

The Core Problem: Speed vs. Stability

Stochastic Gradient Descent (SGD): SGD provides a highly stable and reliable learning process by updating parameters in the direction of the negative gradient: $\theta_{t+1}=\theta_{t}-\eta\nabla J(\theta_{t})$ . However, its convergence speed towards the optimal minimum is notoriously slow.
Nesterov Accelerated Gradient (NAG): NAG offers a much faster convergence rate by utilizing a momentum mechanism that predicts future positions:
$v_{t}=\gamma v_{t-1}+\eta\nabla J(\theta_{t}-\gamma v_{t-1})$ . However, in Mini-Batch environments, this momentum amplifies data noise, leading to extreme instability, oscillations, and sometimes even divergence from the optimal point.

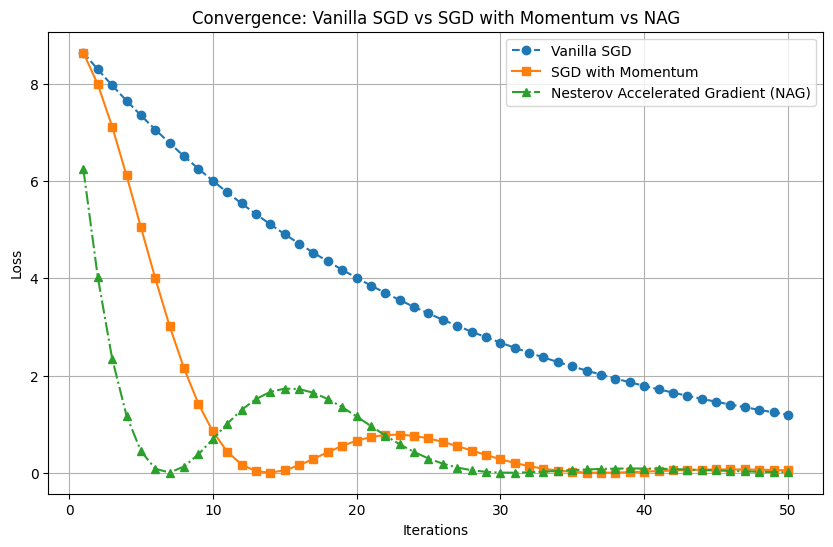SGD vs NAG Comparison (Note: A comparison of SGD's steady but slow descent versus NAG's rapid but oscillatory behavior in a noisy environment.)

The Solution: AGGOA

To solve this, I engineered a hybrid mathematical model: the Adaptive Transition Gradient Optimization Algorithm (AGGOA).

The main philosophy of AGGOA is to dynamically bridge these two methods. It introduces a dynamic transition coefficient ( $S_t$ ) that measures the cost oscillation (instability) during training. Under optimal conditions, AGGOA utilizes the speed of NAG. But the moment it detects high data noise and instability, it dynamically switches to the stable descent of SGD.

By balancing speed and stability, AGGOA aims to provide a more optimal and reliable training environment for deep learning models, proving that mathematical engineering can directly optimize artificial intelligence.